graf
Pod pojmem obyčejný graf G rozumíme uspořádanou dvojicí (V, E) (G = (V, E)), kde V je libovolná množina a E ⊆ P2(V) (P2(V) = všechny dvouprvkové podmnožiny množiny V, prvek množiny E je dvouprvková podmnožina množiny V).
Když jsou množiny V, E konečné, nazýváme graf G konečným, když jsou V, E nekonečné, tak G je nekonečný.
Prvky množiny V budeme nazývat vrcholy, prvky E hrany grafu G.
Každá hrana grafu G je určená dvěma vrcholy, zapisujeme e = {vi,vj}, zkráceně vivj, vi,vj ∈ V, e ∈ E. Počet prvků množiny V značíme n a počet prvků množiny E značíme m (v některé literatuře se můžete setkat s označením |V|= p, |E|= q).
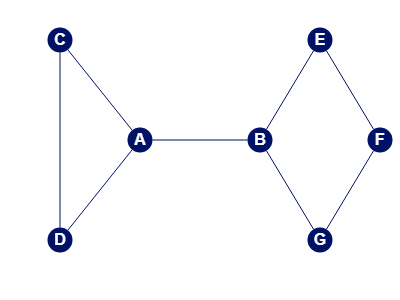
Graf